ปริมาณทางฟิสิกส์
ปริมาณทางฟิสิกส์แบ่งออกได้เป็น 2 ประเภท
1. ปริมาณสเกลาร์ ( Scalar )
คือ ปริมาณที่จะมีแต่ขนาดเท่านั้น ไม่มีทิศทาง การคำนวณสามารถบวก ลบ คูณ หาร ได้ทั่ว ๆ ไป
ตัวอย่าง ปริมาณสเกลาร์ เช่น ระยะทาง ( Distance ) มวล ( Mass ) อัตราเร็ว ( Speed ) ความหนาแน่น ( Density )
2. ปริมาณเวกเตอร์ ( Vector )
คือ ปริมาณที่มีทั้งขนาด และทิศทาง การคำนวณจะใช้วิธีต่าง ๆ ที่แตกต่างจากการคำนวณทั่วไป
ตัวอย่าง ปริมาณเวกเตอร์ เช่น การกระจัด ( Displacement ) แรง ( Force ) ความเร็ว ( Velocity )
ความเร่ง ( Acceleration )
การรวมเวกเตอร์
คือ การบวกหรือลบกันของเวกเตอร์ตั้งแต่ 2 เวกเตอร์ขึ้นไป ผลลัพธ์ที่ได้เป็นปริมาณเวกเตอร์
เรียกว่า เวกเตอร์ลัพธ์ ( Resultant Vector )
มี 2 วิธีดังนี้
1) วิธีวาดรูป ( วิธีหัวต่อหาง )
ทำได้ โดยนำเวกเตอร์ที่เป็นตัวตั้ง จากนั้นเอาหางของเวกเตอร์ที่เป็นผลบวกหรือผลต่าง มาต่อกับหัวของเวกเตอร์ตัวตั้ง
โดยเขียนให้ถูกต้องทั้งขนาดและทิศทาง เวกเตอร์ลัพธ์หาได้จาก หางเวกเตอร์แรก ไปยังหัวเวกเตอร์สุดท้าย

จากรูป ใช้กฏของโคไซน์ ( Cosine's Law ) จะได้ว่า  =
= 
2) วิธีการทางคณิตศาสตร์ ( วิธีการสร้างสี่เหลี่ยมด้านขนาน ) ถ้ามีเวกเตอร์ย่อย 2 อัน สามารถนำมารวมได้โดยแทนขนาดและทิศทาง ด้วยด้านทั้งสองของสี่เหลี่ยมด้านขนาน
ที่ประกอบมุมในจุดนั้น เส้นทแยงมุมที่ลากจากจุดนั้นไปยังมุมตรงข้ามจะแทนทั้งขนาด และทิศทางของเวกเตอร์ลัพธ์

ส่วนการลบเวกเตอร์ให้ทำคล้าย ๆ กันกับการบวกเวกเตอร์เพียงแต่ให้กลับทิศทางของเวกเตอร์ตัวลบ

1. ปริมาณสเกล่าร์ คือปริมาณที่บอกแต่ขนาดอย่างเดียวก็ได้ความหมายสมบูรณ์ ไม่ต้องบอกทิศทาง เช่น ระยะทาง มวล เวลา ปริมาตร ความหนาแน่น งาน พลังงาน ฯลฯ
การหาผลลัพธ์ของปริมาณสเกล่าร์ ก็อาศัยหลังการทางพีชคณิต คือ วิธีการ บวก ลบ คูณ หาร
2. ปริมาณเวกเตอร์ คือ ปริมาณที่ต้องบอกทั้งขนาดและทิศทาง จึงจะได้ความหมายสมบูรณ์ เช่น การกระจัด ความเร่ง ความเร็ว แรง โมเมนตัม ฯลฯ
การหาผลลัพธ์ของปริมาณเวกเตอร์ ต้องอาศัยวิธีการทางเวคเตอร์ โดยต้องหาผลลัพธ์ทั้งขนาดและทิศทาง
1. สัญลักษณ์ของปริมาณเวกเตอร์
ใช้อักษรมีลูกศรครึ่งบนชี้จากซ้ายไปขวา หรือใช้ตัวอักษรทึบแสดงปริมาณเวกเตอร์ก็ได้
2. เวกเตอร์ที่เท่ากัน
เวกเตอร์ 2 เวกเตอร์เท่ากัน เมื่อเวกเตอร์ทั้งสองเท่ากันและมีทิศไปทางเดียวกัน
3. เวกเตอร์ลัพธ์ใช้อักษร R
4. การบวก-ลบเวกเตอร์
การบวก-ลบเวกเตอร์ หรือการหาเวกเตอร์ สามารถทำได้ 2 วิธี คือ
1. วิธีการเขียนรูป
2. วิธีการคำนวณ
1.1 การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบหางต่อหัว มีขั้นตอนดังนี้
(1) เขียนลูกศรตามเวกเตอร์แรกตามขนาดและทิศทางที่กำหนด
(2) นำหางลูกศรของเวกเตอร์ที่ 2 ที่โจทย์กำหนด ต่อหัวลูกศรของเวกเตอร์แรก
(3) นำหางลูกศรของเวกเตอร์ที่ 3 ที่โจทย์กำหนด ต่อหัวลูกศรของเวกเตอร์ที่ 2
(4) ถ้ามีเวกเตอร์ย่อยๆอีก ให้นำเวกเตอร์ต่อๆไป มากระทำดังข้อ (3) จนครบทุกเวกเตอร์
(5) เวกเตอร์ลัพธ์หาได้โดยการลากลูกศรจากหางของเวกเตอร์แรกไปยังหัวของเวกเตอร์สุดท้าย เช่น


ถ้า A เป็นเวกเตอร์ใดๆที่มีขนาดและทิศทางหนึ่งๆ เวกเตอร์ -A คือ เวกเตอร์ที่มีขนาดเท่ากับเวกเตอร์ A แต่ มี ทิศทางตรงกันข้าม
1.2 การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ
เนื่องจากการหาเวกเตอร์ลัพธ์โดยวิธีการวาดรูป ให้ผลลัพธ์ไม่แม่นยำเพียงแต่ได้คร่าวๆ เท่านั้น เพราะถ้าลากความยาวหรือทิศทางลูกศรแทนเวกเตอร์คลาดเคลื่อนเพียงเล็กน้อย ผลของเวกเตอร์ลัพธ์ก็จะคลาดเคลื่อนไปด้วยแต่การหาเวกเตอร์ลัพธ์โดยการคำนวณจะให้ผลลัพธ์ถูกต้องแน่นอน
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ เมื่อมีเวกเตอร์ย่อยเพียง 2 เวกเตอร์ จะแบ่งออกเป็น 3 ลักษณะ ดังนี้
1. เวกเตอร์ทั้ง 2 ไปทางเดียวกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลบวกของขนาดเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ไปทางเดียวกับเวกเตอร์ทั้งสอง
2. เวกเตอร์ทั้ง 2 สวนทางกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลต่างของเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ที่มีขนาดมากกว่า
เพราะฉะนั้น R = B - A เมื่อ B > A , R = A - B เมื่อ A > B
3. เวกเตอร์ทั้ง 2 ทำมุม
ระยะทาง (Distance) คือ ความยาววัดตามแนวเส้นที่อนุภาคเคลื่อนที่ เป็นปริมาณสเกล่าร์(มีเฉพาะขนาด)หน่วยมาตรฐาน SI คือ "เมตร"
การขจัด หรือ การกระจัด (Displacement) คือ เส้นตรงที่ลากจากจุดตั้งต้นของการเคลื่อนที่ไปยังจุดสุดท้ายของการเคลื่อนที่ เป็นปริมาณเวกเตอร์ มีทั้งขนาดและทิศทาง (คือ ทิศจากที่หัวศรลากจากจุดตั้งต้นไปสุดท้าย)มีหน่วย "เมตร" เช่นกัน

แรงและการเคลื่อนที่
1. เวกเตอร์ของแรง แรง (force) หมายถึง สิ่งที่สามารถทำให้วัตถุที่อยู่นิ่งเคลื่อนที่หรือทำให้วัตถุที่กำลังเคลื่อนที่มีความเร็วเพิ่มขึ้นหรือช้าลง หรือเปลี่ยนทิศทางการเคลื่อนที่ของวัตถุได้
ปริมาณทางฟิสิกส์ มี 2 ชนิด คือ
1. ปริมาณเวกเตอร์ (vector quality) หมายถึง ปริมาณที่มีทั้งขนาดและทิศทาง เช่น แรง ความเร็ว ความเร่ง โมเมนต์ โมเมนตัม น้ำหนัก เป็นต้น
2. ปริมาณสเกลาร์ (scalar quality) หมายถึง ปริมาณที่มีแต่ขนาดอย่างเดียว ไม่มีทิศทาง เช่น เวลา พลังงาน ความยาว อุณหภูมิ เวลา พื้นที่ ปริมาตร อัตราเร็ว เป็นต้น
1. ปริมาณเวกเตอร์ (vector quality) หมายถึง ปริมาณที่มีทั้งขนาดและทิศทาง เช่น แรง ความเร็ว ความเร่ง โมเมนต์ โมเมนตัม น้ำหนัก เป็นต้น
2. ปริมาณสเกลาร์ (scalar quality) หมายถึง ปริมาณที่มีแต่ขนาดอย่างเดียว ไม่มีทิศทาง เช่น เวลา พลังงาน ความยาว อุณหภูมิ เวลา พื้นที่ ปริมาตร อัตราเร็ว เป็นต้น
การเขียนเวกเตอร์ของแรง
การเขียนใช้ความยาวของส่วนเส้นตรงแทนขนาดของแรง และหัวลูกศรแสดงทิศทางของแรง
การเขียนใช้ความยาวของส่วนเส้นตรงแทนขนาดของแรง และหัวลูกศรแสดงทิศทางของแรง
2. การเคลื่อนที่ในหนึ่งมิติ
2.1 การเคลื่อนที่ในแนวเส้นตรง แบ่งเป็น 2 แบบ คือ
1. การเคลื่อนที่ในแนวเส้นตรงที่ไปทิศทางเดียวกันตลอด เช่น โยนวัตถุขึ้นไปตรงๆ รถยนต์ กำลังเคลื่อนที่ไปข้างหน้าในแนวเส้นตรง
2. การเคลื่อนที่ในแนวเส้นเส้นตรง แต่มีการเคลื่อนที่กลับทิศด้วย เช่น รถแล่นไปข้างหน้าในแนวเส้นตรง เมื่อรถมีการเลี้ยวกลับทิศทาง ทำให้ทิศทางในการเคลื่อนที่ตรงข้ามกัน
2.2 อัตราเร็ว ความเร่ง และความหน่วงในการเคลื่อนที่ของวัตถุ 1. อัตราเร็วในการเคลื่อนที่ของวัตถุ คือระยะทางที่วัตถุเคลื่อนที่ใน 1 หน่วยเวลา
2. ความเร่งในการเคลื่อนที่ หมายถึง ความเร็วที่เพิ่มขึ้นใน 1 หน่วยเวลา เช่น วัตถุตกลงมาจากที่สูงในแนวดิ่ง
3. ความหน่วงในการเคลื่อนที่ของวัตถุ หมายถึง ความเร็วที่ลดลงใน 1 หน่วยเวลา เช่น โยนวัตถุขึ้นตรงๆ ไปในท้องฟ้า
3. การเคลื่อนที่แบบต่างๆ ในชีวิตประจำวัน
3.1 การเคลื่อนที่แบบวงกลม หมายถึง การเคลื่อนที่ของวัตถุเป็นวงกลมรอบศูนย์กลาง เกิดขึ้นเนื่องจากวัตถุที่กำลังเคลื่อนที่จะเดินทางเป็นเส้นตรงเสมอ แต่ขณะนั้นมีแรงดึงวัตถุเข้าสู่ศูนย์กลางของวงกลม เรียกว่า แรงเข้าสู่ศูนย์กลางการเคลื่อนที่ จึงทำให้วัตถุเคลื่อนที่เป็นวงกลมรอบศูนย์กลาง เช่น การโคจรของดวงจันทร์รอบโลก
3.2 การเคลื่อนที่ของวัตถุในแนวราบ เป็นการเคลื่อนที่ของวัตถุขนานกับพื้นโลก เช่น รถยนต์ที่กำลังแล่นอยู่บนถนน
3.3 การเคลื่อนที่แนววิถีโค้ง เป็นการเคลื่อนที่ผสมระหว่างการเคลื่อนที่ในแนวดิ่งและในแนวราบ
3.1 การเคลื่อนที่แบบวงกลม หมายถึง การเคลื่อนที่ของวัตถุเป็นวงกลมรอบศูนย์กลาง เกิดขึ้นเนื่องจากวัตถุที่กำลังเคลื่อนที่จะเดินทางเป็นเส้นตรงเสมอ แต่ขณะนั้นมีแรงดึงวัตถุเข้าสู่ศูนย์กลางของวงกลม เรียกว่า แรงเข้าสู่ศูนย์กลางการเคลื่อนที่ จึงทำให้วัตถุเคลื่อนที่เป็นวงกลมรอบศูนย์กลาง เช่น การโคจรของดวงจันทร์รอบโลก
3.2 การเคลื่อนที่ของวัตถุในแนวราบ เป็นการเคลื่อนที่ของวัตถุขนานกับพื้นโลก เช่น รถยนต์ที่กำลังแล่นอยู่บนถนน
3.3 การเคลื่อนที่แนววิถีโค้ง เป็นการเคลื่อนที่ผสมระหว่างการเคลื่อนที่ในแนวดิ่งและในแนวราบ
กฎการเคลื่อนที่ของนิวตัน
นิวตัน ได้สรุปหลักการเกี่ยวกับการเคลื่อนที่ของวัตถุทั้งที่อยู่ในสภาพอยู่นิ่งและในสภาพเคลื่อนที่ ดังนี้
นิวตัน ได้สรุปหลักการเกี่ยวกับการเคลื่อนที่ของวัตถุทั้งที่อยู่ในสภาพอยู่นิ่งและในสภาพเคลื่อนที่ ดังนี้
กฎข้อที่ 1 วัตถุถ้าหากว่ามีสภาพหยุดนิ่งหรือเคลื่อนที่เป็นเส้นตรงด้วยความเร็วคงที่ มันยังจะคงสภาพเช่นนี้ต่อไป หากไม่มีแรงที่ไม่สมดุลจากภายนอกมากระทำ
กฎข้อที่ 2 ถ้าหากมีแรงที่ไม่สมดุลจากภายนอกมากระทำต่อวัตถุ แรงที่ไม่สมดุลนั้นจะเท่ากับอัตราการเปลี่ยนแปลงโมเมนต์ตัมเชิงเส้นของวัตถุ
กฎข้อที่ 3 ทุกแรงกริยาที่กระทำ จะมีแรงปฏิกิริยาที่มีขนาดที่เท่ากันแต่มีทิศทางตรงกันข้ามกระทำตอบเสมอ
กฎการเคลื่อนที่ข้อที่ 1 และข้อที่ 3 เราได้ใช้ในการศึกษาในวิชาสถิตยศาสตร์ มาแล้วสำหรับในการศึกษาพลศาสตร์ เราจึงสนใจในกฎการเคลื่อนที่ข้อที่สองมากกว่า
แรงในแบบต่างๆ
1. ชนิดของแรง
1.1 แรงย่อย คือ แรงที่เป็นส่วนประกอบของแรงลัพธ์
1.2 แรงลัพธ์ คือ แรงรวมซึ่งเป็นผลรวมของแรงย่อย ซึ่งจะต้องเป็นการรวมกันแบบปริมาณเวกเตอร์
1.3 แรงขนาน คือ แรงที่ที่มีทิศทางขนานกัน ซึ่งอาจกระทำที่จุดเดียวกันหรือต่างจุดกันก็ได้ มีอยู่ 2 ชนิด
- แรงขนานพวกเดียวกัน หมายถึง แรงขนานที่มีทิศทางไปทางเดียวกัน
- แรงขนานต่างพวกกัน หมายถึง แรงขนานที่มีทิศทางตรงข้ามกัน
1.4 แรงหมุน หมายถึง แรงที่กระทำต่อวัตถุ ทำให้วัตถุเคลื่อนที่โดยหมุนรอบจุดหมุน ผลของการหมุนของ เรียกว่า โมเมนต์ เช่น การปิด-เปิด ประตูหน้าต่าง 1.5 แรงคู่ควบ คือ แรงขนานต่างพวกกันคู่หนึ่งที่มีขนาดเท่ากัน แรงลัพธ์มีค่าเป็นศูนย์ และวัตถุที่ถูกแรงคู่ควบกระทำ 1 คู่กระทำ จะไม่อยู่นิ่งแต่จะเกิดแรงหมุน 1.6 แรงดึง คือ แรงที่เกิดจากการเกร็งตัวเพื่อต่อต้านแรงกระทำของวัตถุ เป็นแรงที่เกิดในวัตถุที่ลักษณะยาวๆ เช่น เส้นเชือก เส้นลวด 1.7 แรงสู่ศูนย์กลาง หมายถึง แรงที่มีทิศเข้าสู่ศูนย์กลางของวงกลมหรือทรงกลมอันหนึ่งๆ เสมอ 1.8 แรงต้าน คือ แรงที่มีทิศทางต่อต้านการเคลื่อนที่หรือทิศทางตรงข้ามกับแรงที่พยายามจะทำให้วัตถุเกิดการเคลื่อนที่ เช่น แรงต้านของอากาศ แรงเสียดทาน 1.9 แรงโน้มถ่วงของโลก คือ แรงดึงดูดที่มวลของโลกกระทำกับมวลของวัตถุ เพื่อดึงดูดวัตถุนั้นเข้าสู่ศูนย์กลางของโลก
- น้ำหนักของวัตถุ เกิดจากความเร่งเนื่องจากความโน้มถ่วงของโลกมากกระทำต่อวัตถุ 1.10 แรงกิริยาและแรงปฏิกิริยา
- แรงกิริยา คือ แรงที่กระทำต่อวัตถุที่จุดจุดหนึ่ง อาจเป็นแรงเพียงแรงเดียวหรือแรงลัพธ์ของแรงย่อยก็ได้
- แรงปฏิกิริยา คือ แรงที่กระทำตอบโต้ต่อแรงกิริยาที่จุดเดียวกัน โดยมีขนาดเท่ากับแรงกิริยา แต่ทิศทางของแรงทั้งสองจะตรงข้ามกัน
2. แรงกิริยาและแรงปฏิกิริยากับการเคลื่อนที่ของวัตถุ
2.1 วัตถุเคลื่อนที่ด้วยแรงกิริยา เป็นการเคลื่อนที่ของวัตถุตามแรงที่กระทำ เช่น การขว้างลูกหินออกไป
2.2 วัตถุเคลื่อนที่ด้วยแรงปฏิกิริยา เป็นการเคลื่อนที่ของวัตถุเนื่องจากมีแรงขับดันวัตถุให้เคลื่อนที่ไปในทิศทางตรงกันข้าม เช่น การเคลื่อนที่ของจรวด
1.1 แรงย่อย คือ แรงที่เป็นส่วนประกอบของแรงลัพธ์
1.2 แรงลัพธ์ คือ แรงรวมซึ่งเป็นผลรวมของแรงย่อย ซึ่งจะต้องเป็นการรวมกันแบบปริมาณเวกเตอร์
1.3 แรงขนาน คือ แรงที่ที่มีทิศทางขนานกัน ซึ่งอาจกระทำที่จุดเดียวกันหรือต่างจุดกันก็ได้ มีอยู่ 2 ชนิด
- แรงขนานพวกเดียวกัน หมายถึง แรงขนานที่มีทิศทางไปทางเดียวกัน
- แรงขนานต่างพวกกัน หมายถึง แรงขนานที่มีทิศทางตรงข้ามกัน
1.4 แรงหมุน หมายถึง แรงที่กระทำต่อวัตถุ ทำให้วัตถุเคลื่อนที่โดยหมุนรอบจุดหมุน ผลของการหมุนของ เรียกว่า โมเมนต์ เช่น การปิด-เปิด ประตูหน้าต่าง 1.5 แรงคู่ควบ คือ แรงขนานต่างพวกกันคู่หนึ่งที่มีขนาดเท่ากัน แรงลัพธ์มีค่าเป็นศูนย์ และวัตถุที่ถูกแรงคู่ควบกระทำ 1 คู่กระทำ จะไม่อยู่นิ่งแต่จะเกิดแรงหมุน 1.6 แรงดึง คือ แรงที่เกิดจากการเกร็งตัวเพื่อต่อต้านแรงกระทำของวัตถุ เป็นแรงที่เกิดในวัตถุที่ลักษณะยาวๆ เช่น เส้นเชือก เส้นลวด 1.7 แรงสู่ศูนย์กลาง หมายถึง แรงที่มีทิศเข้าสู่ศูนย์กลางของวงกลมหรือทรงกลมอันหนึ่งๆ เสมอ 1.8 แรงต้าน คือ แรงที่มีทิศทางต่อต้านการเคลื่อนที่หรือทิศทางตรงข้ามกับแรงที่พยายามจะทำให้วัตถุเกิดการเคลื่อนที่ เช่น แรงต้านของอากาศ แรงเสียดทาน 1.9 แรงโน้มถ่วงของโลก คือ แรงดึงดูดที่มวลของโลกกระทำกับมวลของวัตถุ เพื่อดึงดูดวัตถุนั้นเข้าสู่ศูนย์กลางของโลก
- น้ำหนักของวัตถุ เกิดจากความเร่งเนื่องจากความโน้มถ่วงของโลกมากกระทำต่อวัตถุ 1.10 แรงกิริยาและแรงปฏิกิริยา
- แรงกิริยา คือ แรงที่กระทำต่อวัตถุที่จุดจุดหนึ่ง อาจเป็นแรงเพียงแรงเดียวหรือแรงลัพธ์ของแรงย่อยก็ได้
- แรงปฏิกิริยา คือ แรงที่กระทำตอบโต้ต่อแรงกิริยาที่จุดเดียวกัน โดยมีขนาดเท่ากับแรงกิริยา แต่ทิศทางของแรงทั้งสองจะตรงข้ามกัน
2. แรงกิริยาและแรงปฏิกิริยากับการเคลื่อนที่ของวัตถุ
2.1 วัตถุเคลื่อนที่ด้วยแรงกิริยา เป็นการเคลื่อนที่ของวัตถุตามแรงที่กระทำ เช่น การขว้างลูกหินออกไป
2.2 วัตถุเคลื่อนที่ด้วยแรงปฏิกิริยา เป็นการเคลื่อนที่ของวัตถุเนื่องจากมีแรงขับดันวัตถุให้เคลื่อนที่ไปในทิศทางตรงกันข้าม เช่น การเคลื่อนที่ของจรวด
ระยะทาง
ระยะทาง หมายถึงตัวเลขที่อธิบายว่า วัตถุแต่ละอย่างอยู่ห่างกันเท่าไรในช่วงเวลาหนึ่ง ในทางฟิสิกส์ ระยะทางอาจหมายถึงความยาวทางกายภาพ ระยะเวลา หรือการประมาณค่าบนสิ่งที่พิจารณาสองอย่าง ส่วนทางคณิตศาสตร์จะพิจารณาอย่างเฉพาะเจาะจงมากกว่า โดยทั่วไปแล้ว "ระยะทางจาก A ไป B" มีความหมายเหมือนกับ "ระยะทางระหว่าง A กับ
ในเรขาคณิตสัมบูรณ์ (absolute geometry) ระยะทางที่น้อยที่สุดระหว่างจุดสองจุด คือความยาวของส่วนของเส้นตรงที่เชื่อมระหว่างจุดเหล่านั้น
ในเรขาคณิตเชิงพีชคณิต (algebraic geometry) เราสามารถหาระยะทางระหว่างจุดสองจุดบนระนาบ xy โดยใช้สูตรต่อไปนี้ ระยะทางจาก (x1, y1) ไปยัง (x2, y2) คำนวณได้จาก
ในการศึกษาเรขาคณิตในระดับที่ซับซ้อน เราจะเรียกการหาระยะทางแบบนี้ว่าเป็น ระยะทางแบบยุคลิด (Euclidean distance) ซึ่งขยายผลมาจากทฤษฎีบทพีทาโกรัส แต่จะไม่ครอบคลุมถึงเรขาคณิตนอกแบบยุคลิด (non-Euclidean geometry) สูตรการหาระยะทางข้างต้นสามารถนำไปประยุกต์ใช้กับความยาวส่วนโค้ง (arc length) ได้ด้วย
[แก้] กรณีทั่วไป
ฟังก์ชันระยะทาง d บนเซต M ที่เป็นเซตของจุด กำหนดขึ้นโดยที่ d : M×M → ℝ จะทำให้เงื่อนไขต่อไปนี้เป็นจริง- d(x, y) ≥ 0 และ d(x, y) = 0 ก็ต่อเมื่อ x = y (ระยะทางระหว่างจุดสองจะเป็นจำนวนบวก และจะเป็นศูนย์ก็ต่อเมื่ออยู่ที่จุดเดียวกัน)
- d(x, y) = d(y, x) (ระยะทางระหว่างจุดสองจุดจะเท่ากันโดยไม่คิดทิศทาง)
- d(x, z) ≤ d(x, y) + d(y, z) (ระยะทางระหว่างจุดสองจุด จะสั้นกว่าหรือเท่ากับระยะทางรวมที่ผ่านจุดอื่น)
การกระจัด
จากวิกิพีเดีย สารานุกรมเสรี
การกระจัด หรือ การขจัด คือระยะทางที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดสิ้นสุด [1] ระยะทางที่สั้นที่สุดก็คือความยาวของเส้นตรงสมมติที่ลากจากจุดเริ่มต้นไปยังจุดสิ้นสุด ดังนั้นมันจึงอาจแตกต่างจากเส้นทางเดินปกติก็ได้ เวกเตอร์การกระจัด ก็คือความยาวและทิศทางของเส้นตรงสมมติดังกล่าว
เวกเตอร์ตำแหน่งเป็นตัวบ่งชี้ตำแหน่งของจุด P ในปริภูมิ ซึ่งเกี่ยวข้องกับการกระจัดจากจุดอ้างอิง O (โดยทั่วไปจะเป็นจุดกำเนิดของระบบพิกัด) เวกเตอร์ตำแหน่งแสดงให้เห็นว่า ถ้าเคลื่อนที่ไปในแนวเส้นตรงโดยเริ่มจากจุด O ด้วยระยะทางและทิศทางนั้น ก็จะพบกับจุด P ที่ปลายทาง
การกระจัดอาจถูกเรียกว่าเป็น เวกเตอร์ตำแหน่งสัมพัทธ์ กล่าวคือ เมื่อเวกเตอร์ตำแหน่งสิ้นสุด Rf สัมพันธ์กับเวกเตอร์ตำแหน่งเริ่มต้น Ri เวกเตอร์การกระจัดสามารถนิยามขึ้นได้จากผลต่างระหว่างเวกเตอร์สิ้นสุดกับเวกเตอร์เริ่มต้น ดังนี้ (สัญกรณ์ตัวหนาหมายถึงเวกเตอร์)
เวกเตอร์ตำแหน่งเป็นตัวบ่งชี้ตำแหน่งของจุด P ในปริภูมิ ซึ่งเกี่ยวข้องกับการกระจัดจากจุดอ้างอิง O (โดยทั่วไปจะเป็นจุดกำเนิดของระบบพิกัด) เวกเตอร์ตำแหน่งแสดงให้เห็นว่า ถ้าเคลื่อนที่ไปในแนวเส้นตรงโดยเริ่มจากจุด O ด้วยระยะทางและทิศทางนั้น ก็จะพบกับจุด P ที่ปลายทาง
การกระจัดอาจถูกเรียกว่าเป็น เวกเตอร์ตำแหน่งสัมพัทธ์ กล่าวคือ เมื่อเวกเตอร์ตำแหน่งสิ้นสุด Rf สัมพันธ์กับเวกเตอร์ตำแหน่งเริ่มต้น Ri เวกเตอร์การกระจัดสามารถนิยามขึ้นได้จากผลต่างระหว่างเวกเตอร์สิ้นสุดกับเวกเตอร์เริ่มต้น ดังนี้ (สัญกรณ์ตัวหนาหมายถึงเวกเตอร์)

- อัตราเร็ว
- (สัญลักษณ์: v) คืออัตราของ การเคลื่อนที่ หรือ อัตราการเปลี่ยนแปลงของตำแหน่งก็ได้ หลายครั้งมักเขียนในรูป ระยะทาง d ที่เคลื่อนที่ไปต่อ หน่วย ของ เวลา t
อัตราเร็ว เป็นปริมาณสเกลาร์ที่มีมิติเป็นระยะทาง/เวลา ปริมาณเวกเตอร์ที่เทียบเท่ากับอัตราเร็วคือความเร็ว อัตราเร็ววัดในหน่วยเชิงกายภาพเดียวกับความเร็ว แต่อัตราเร็วไม่มีองค์ประกอบของทิศทางแบบที่ความเร็วมี อัตราเร็วจึงเป็นองค์ประกอบส่วนที่เป็นขนาดของความเร็ว
ในรูปสัญลักษณ์ทางคณิตศาสตร์ อัตราเร็วคือ
- เมตรต่อวินาที, (สัญลักษณ์ m/s) , ระบบหน่วย SI
- กิโลเมตรต่อชั่วโมง, (สัญลักษณ์ km/h)
- ไมล์ต่อชั่วโมง, (สัญลักษณ์ mph)
- นอต (ไมล์ทะเลต่อชั่วโมง, สัญลักษณ์ kt)
- มัค เมื่อมัค 1 เท่ากับ อัตราเร็วเสียง มัค n เท่ากับ n เท่าของอัตราเร็วเสียง
-
- มัค 1 ≈ 343 m/s ≈ 1235 km/h ≈ 768 mi/h (ดู อัตราเร็วเสียง สำหรับข้อมูลเพิ่มเติม)
- อัตราเร็วแสง ใน สุญญากาศ (สัญลักษณ์ c) เป็นหนึ่งใน หน่วยธรรมชาติ
-
- c = 299,792,458 m/s
- การเปลี่ยนหน่วยที่สำคัญ
-
- 1 m/s = 3.6 km/h
- 1 mph = 1.609 km/h
- 1 knot = 1.852 km/h = 0.514 m/s
วัตถุที่เคลื่อนที่ไปตามแนวราบ พร้อม ๆ กับแนวดิ่ง (เช่น อากาศยาน) จะแยกประเภทเป็น forward speed กับ climbing speed
เนื้อหา
[ซ่อน][แก้] อัตราเร็วเฉลี่ย
อัตราเร็วในรูป สมบัติเชิงกายภาพ มักแทนอัตราเร็วที่ขณะใดขณะหนึ่ง ในชีวิตจริงเรามันใช้ อัตราเร็วเฉลี่ย (ใช้สัญลักษณ์ ) ซึ่งก็คือ อัตรา ของ ระยะทาง รวม (หรือ ความยาว) ต่อช่วง เวลา
) ซึ่งก็คือ อัตรา ของ ระยะทาง รวม (หรือ ความยาว) ต่อช่วง เวลา
ยกตัวอย่างเช่น ถ้าคุณเคลื่อนที่ได้ 60 ไมล์ในเวลา 2 ชั่วโมง อัตราเร็ว เฉลี่ย ของคุณในช่วงเวลานั้นคือ 60/2 = 30 ไมล์ต่อชั่วโมง แต่อัตราเร็วที่ขณะใดขณหนึ่งย่อมเปลี่ยนแปลงต่างกันไป
ในรูปสัญลักษณ์ทางคณิตศาสตร์
![[t_0, t_1]](http://upload.wikimedia.org/wikipedia/th/math/0/b/3/0b3b8cb99d808fe833d8f1c61cac6b2e.png) จะให้อัตราเร็วเฉลี่ยในรูป
จะให้อัตราเร็วเฉลี่ยในรูป
![[l_0, l_1]](http://upload.wikimedia.org/wikipedia/th/math/8/7/2/8722996cc2ef22ea31fa9b4bd65b734f.png) จะให้อัตราเร็วเฉลี่ยในรูป
จะให้อัตราเร็วเฉลี่ยในรูป
 และระยะทางครึ่งที่สองด้วยอัตราเร็ว
และระยะทางครึ่งที่สองด้วยอัตราเร็ว  จะให้อัตราเร็วเฉลี่ยรวมเป็น
จะให้อัตราเร็วเฉลี่ยรวมเป็น  ค่าที่ถูกต้องต้องเป็น
ค่าที่ถูกต้องต้องเป็น 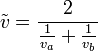
(ระลึกไว้ว่า อย่างแรกเป็น ค่าเฉลี่ยเลขคณิต ในขณะที่อย่างที่สองเป็น ค่าเฉลี่ยฮาร์มอนิก)
อัตราเร็วเฉลี่ยสามารถหาได้จาก distribution function ของอัตราเร็วได้เช่นกัน (ทั้งในรูประยะทางหรือเวลาก็ตาม)










